何为量子计算机?
本文最后更新于:2019年12月15日 凌晨
目前阶段,只能够集成几十个量子比特的阶段,但是整个量子计算领域还是非常受资本市场的追捧的。
从目前2019来看,公认的几大潜在基础设施爆炸,站在最风口的: 5G(低延时、高速度、高稳定);AI赋能。
这些都其意味着远程交互的可行性、多传感器交互与智能化,对应的是新移动(如车联网)、智能空间(智能家居、智能书房、远程手术台、VR、AR..)。
而在当下研究更加长远一点颠覆性的但具有可行性技术非量子计算(计算力的指数增长)莫属了,无论是美国中国都在这块举国之力投入,其对应的是更加宏观的预测、加密技术的飞跃发展,可能意味着整个人类社会”进入另一个纪元”。
我们先从上段时间谷歌声称量子霸权说起…
I. 谷歌的量子霸权
看伊万卡这发的,不懂的还以为美国要申明自己要独霸一方了呢,虽然好像本来就是…
谷歌做了什么声称量子霸权?
量子霸权来源: 2012年 加州理工学院的理论物理学家、量子信息与物质研究所所长约翰·普雷斯基尔(John Preskill)提出在特定问题上一个量子计算机只要量子比特超过50个就会远超经典计算机,那个时候就是量子霸权时代了。
谷歌采用了相对其他方式简单一些的随机量子线路采样设计了量子电路(Sycamore量子芯片),让53个量子比特都能够足够随机,在多项式时间内实现了200s就能采样到100w次的随机数(电路采样次数),而选用最佳的算法在最强超算Summit上估算需要至少1万年,根据定义确实是远超经典计算机,并且超过了50个量子比特。从结果上来看确实就是之前Preskill提到的量子霸权。
从各大平台上看,这虽然应用场景比较有限,但是依然是具有里程碑意义的事情,不过针对这一情况,在量子计算方面同样是大佬的IBM似乎有些不爽,发文质疑说如果考虑大量磁盘的情况,最坏情况所谓的超级计算机1w年的计算量,经典计算机2.5天就能完成,2333..
谷歌做的随机数?
这里我们提到了谷歌用量子计算机输出大量随机数,那么什么是随机数,与我们常见的经典计算机终有什么差别呢?
我们通常在经典计算机中生成的随机数都是通过固定算法生成的伪随机,比如:
- Pi的后x位开始每次给一个数
- 比如使用线性同余公式对48位的种子进行修改(Java Random: 种子为
System.currentTimeMillis()) - 比如使用从1970.1.1到目前的毫秒数对一些数取模
- ..
伪随机都有一个特征,那就是都可以通过相同的输入返回相同的”随机数”,而用量子计算我们却可以得到真随机,什么是真随机呢,比如:
- 反射元素半衰期
- 电子元件的噪音
- 记录骰子的情况
真随机的特征就是无法预知,这也是量子计算机的天然优势,由于量子的特征,随机对齐来说就是天然的,这里并不是说谷歌不牛逼,要做到足够随机、侦测以及如何落地是非常困难的事情,甚至之前谷歌已经有了72个量子比特的实验,谷歌在量子计算机领域在业界是领导性的地位,至于为什么提到53个量子比特做个随机数就困难呢,我们继续往下看。
II. 什么是量子计算机?
迪文森佐标准定义量子计算机
- 良好表征(每个支持单独寻址)的量子比特,并可拓展(可集成): 目前已有技术方案,正在进一步研究,后文会提到
- 必须有方法在计算前将所有量子比特设置为0: 目前只能对每个量子比特单独处理,当多了以后目前还没有办法批量处理
- 必须有通用的量子逻辑门: 目前已有通用门,其分为双量子比特的受控非门(通过量子纠缠实现)与单量子比特门
- 要有有效的退相干办法: 目前有多种量子编码原理可以解决,后文会提到
- 要能通过测量获得量子比特得到想要的答案: 目前还无法说通过计算后的量子比特就立马得出100%的答案,都是趋近准确,通过提高测量次数来提高准确度
对于迪文森佐定义的标准,我们可以看到目前绝大多数都有理论支持至少理论可行,或者有很多都通过了实验验证可行,因此量子计算机绝不是空谈。
量子天然优势 – 并行计算
量子计算机的中的存储单元是量子比特(qubit),就如同经典计算机的比特(bit),而与比特最大的不同是量子比特拥有叠加态,也就是每个qubit可以同时表达1与0:
n个qubit: 可同时表示2^n个数n个bit: 可同时表示1个数
我们可以理解基本的形态:
- 经典计算机: 多个固定状态的bit组合
- 量子计算机: 每个qubit可以表达2种状态
为了便于理解,下面是一个简单的案例:
- 1个
qubit可同时表示:0、1(经典需要1bit只能取两种之一) - 2个
qubit可同时表示:00、01、10、11(经典需要2bit只能取四种之一)
III. 量子计算机有什么用呢?
Hamilton回路: 给你一个图,能否找到一条经过每个顶点一次且恰好一次最后又走回来的路
这个是第一次接触量子计算机最容易被提出的问题,如果你用经典计算机的想法来理解量子计算机就会进入经典计算机的漩涡,在了解量子计算机之前我们先了解下多项式时间、P、NP、NPC这几个概念:
- 多项式(Polynomial)时间: 类似O(1)、O(log(n))、O(n^a),它的
n出现在底数位置;当问题规模变大后,程序需要的时间增长的速度通常不会很大是很有限的 - P(Polynomial)问题: 能在多项式时间里解决它的问题
- NP问题: 不能在多项式时间里解决它,但是可以在多项式时间里验证它(比如问: 从起点到终点是否有一条小于100长度路线,此时如果有人给出一条正确的路线,我们只需要验证它小于100的路径即可验证,验证路线的复杂度是在多项式时间内的)
- NPC(Completely)问题: NP-完全问题,该类问题是NP问题,并且所有NP问题都可以用它证明(比如问: 是否图中不存在Hamilton回路,很显然除非试过所有回路,要不不敢断定没有,但是可以再复杂到(旅行商问题)TSP问题,存在Hamilton回路当且仅当TSP问题中存在长为0的回路(两点相连定义为距离为0),因此Hamilton问题只不过是TSP问题的子集,我们称TSP问题是NPC问题)
这里的NPC还牵扯到”约化”,为了篇幅,这里就不拓展,可以简单的理解如果说存在一个问题B的解可以用来验证问题A,那么就理解问题A可约化为问题B(比如一元二次方程里面的值稍作修改就等价为一元一次方程),实际验证是一个问题约化为另一个问题,时间复杂度增加(如一元二次方程相比一元一次方程复杂度增加),但是应用范围也增加了,通过对问题不断约化,比如P约化为NP问题,NP问题最后不断约化,直到约化为一个复杂度非常高的问题可以通吃所有问题,那么这个问题就是NPC问题。
现在我们再回过头来看量子计算机有什么用呢?可能你已经猜到了量子计算机在解决计算量需要指数增长的问题是拥有先天优势,如NP或者NPC问题,因为量子计算机是并行处理,并且算力随着量子比特数量的增加是叠加指数增长的(2^n),我们可以简单来说:
- 经典计算机用于处理简单的线性问题独立处理,通常可以应付P问题与少数NP问题(量很小的情况)
- 量子计算机用于大量并行的事务,如NP、NPC问题或者是混沌系统问题,其并行体现在比如10000以内的质数一次除完,然后处理下一批,这种问题量子计算机比经典计算机快2^n次方倍(每多一个qubit速度就可以翻一番)
我们举几个经典的量子计算机处理问题的案例:
秀尔(shor)算法 – 大数质因数分解
大数大数质因数分解是一个NP问题,在经典算法中它的复杂度不能够在多项式时间内完成,因此几乎是无法完成的,这也是RSA加密算法的根本:
- 一般的大数质因数分解算法,复杂度: O(e^n) (n是指二进制表示位数个数);300位(十进制)质因数分解需要从宇宙大爆炸计算到现在
- 秀尔算法在量子计算中可以将复杂度降为: O((logN)^3),多项式时间,变为了P类问题;300位(十进制)质因数分解只需要1分钟
该算法已经被验证该算法可行,但是也不用太担心:
- 如果需要破解目前位数的RSA-2048至少需要数百万的量子比特,现在还是几十的数量级距离数百万至少还需要十几年甚至几十年时间
- 当真的达到可破解RSA的算力后,肯定会有更复杂的加密算法出现
快递员问题
这些就是常见的NPC问题: 一个快递员每天要送n个货,n个货彼此之间的距离都是已知,快递员,怎么走才能一遍送完所有快递然后总路程最短
这类问题经典计算机素手无策,只能暴力求解。量子计算机同时计算多路径之和,问题将变为可解决
混沌系统问题
混沌系统问题将与实际的世界息息相关:
- 三体问题
- 天气预报
- 地震预报
- 蛋白质折叠问题
我们生活的世界实际上就是一些列的混沌系统组成的,在经典计算机面前其由于存在巨大的变量与不确定性无法进行计算,但是在量子计算机面前这些的计算都将会成为可能。
IV. 量子计算机的历史起因
这个要从经典计算机说起,如下图:
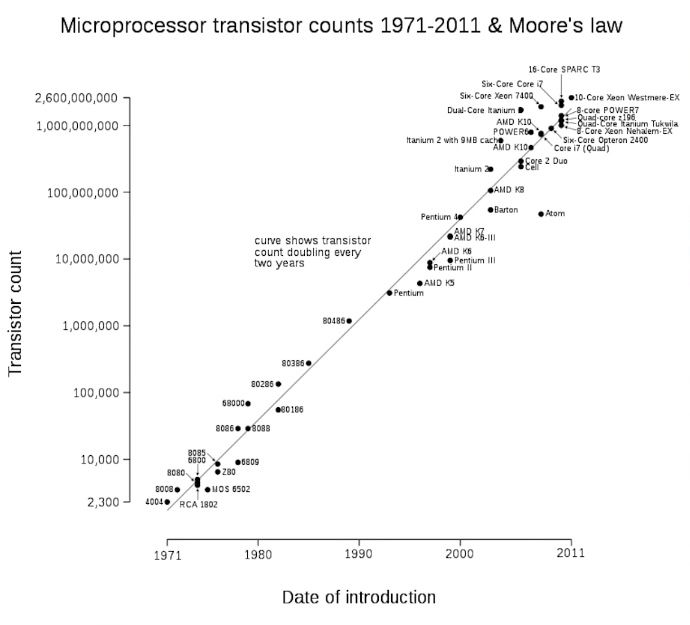
根据摩尔定律,半导体芯片,单位面积上所集成的晶体管和电阻的数量每18个月翻一番,随着时间的的流逝,到目前为止极高的集成度引发的问题可能会需要跳出经典物理领域,这类问题我们可以归结为以下两个:
- 晶体管的体积小到一定的时候就不再遵循经典理论,而是遵循量子力学
- 晶体管集成度的提高导致发热问题严重
针对于微观下的量子力学本篇文章我们不做科普,我们先来看看对于发热问题。我们先来看看芯片发热的来源,根据Landauer原理,每删除一个bit信息会产生kTlog2热量(k: 玻尔兹曼常数;T环境温度),也就是丢失数据会产生热量,放在逻辑门中:
- 可逆门,可任意反推,比如: 非门(
1=!1,!1=1) - 不可逆门,不可任意反推,比如与门(
1&0=0,结果0可以倒推出0&0也可以1&0因此无法准确倒推)
因为不可逆门会产生热量,而实际的经典计算机中存在大量的不可逆门,因此发热是无法避免的,在此期间科学家提出了很多方案:
- 幺正变换
- Fredkin门(把所有的输入输出都改为三个,其中一个控制通道)
- 半加器(^与&组成)
这些做法都是将不可逆门转变为可逆门进行处理,此时物理学家费曼提出为什么不直接将经典比特换成量子比特,这样啥都省了,并且想要了解量子的本质,实际上是无法通过经典计算机进行模拟的,当时原本就有量子计算机的研究,这种变通的思想也进一步推进了量子计算机的发展。
V. 量子计算机目前存在的问题的解决方案,为何量子计算机可行?
量子计算机结果随机出现无法有正确结果,为何能够得到正确答案?
彼得·秀尔,提供了大数质因数分解的量子计算算法,该算法结果是需要的数据相干相长,不需要的数据相干相消,最后测量正确结果的概率是1,因此证明存在算法是可以得到正确答案的。
量子相干性很难保持,如何让其保持?
由于量子纠缠,使得原本不确定的状态(叠加态)变为确定,就变为经典的了,俗称: 波函数坍缩,过程叫做 量子退相干,如果变为了经典那就没有量子什么事了,应该怎么让其保持呢,这块已经有了很多解决方案,我们统称为量子编码,下面我们就来看看常见的几种:
方案一: 量子纠错码
量子纠错码是通过牺牲资源的方式,8个量子比特位做一个用,少数错误服从多数,纠正过来,这种纠错码(纠错量子比特越多,结果越精确)的方式是可行,因为并行计算优势太大了,这种多投入资源简直可以忽略不计,其衍生有:
- CSS纠错码
- 拓扑量子
方案二: 量子避错码
中科大院士郭光灿和其团队1997年提出
这类方式是需要在超辐射环境下,此时量子可以保持很好的相干性,国际上基于该理论提出了”无消相干子空间”,该空间里qubit不会退相干。
方案三: 量子防错码
该方案使用的手段是量子芝诺效应,其适用范围: 两能级体系的量子(基态和激发态,正常是趋于基态(最低能量态)),通过一定频率的测量,来让量子保持在激发态。
物理层面上用什么来做量子比特?
DARPA成功案例: 提出并投资互联网, 投资Unix系统,提出并投资GPS
我们知道在经典物理中,我们使用半导体来作为比特的媒介,那么在量子计算机中我们应该如何表达量子比特呢,理论上所有的两能级都可以做量子比特的媒介,如电子自旋,光子偏振。
但是要保持保持相干性的同时可以做到高集成化,需要一些特殊的处理,目前有一些比较常见的方案:
- 核磁共振: 该方案在2001年成功演示,主要用于演示,只能用于少量的量子比特不能集成化:该演示是IBM华裔研究人员埃塞克·庄做的秀尔算法演示(5个氟原子+2个碳原子=一个分子;利用原子核自旋做量子比特;7qubit = 2^7bit = 128bit)(15的质因数分解,结果3和5)
- 离子阱: 很难集成化,但相干性好,少量的qubit实现容易
- 线性光学: 很难集成化,但相干性好,少量的qubit实现容易;直接用光子偏振,还可验证量子纠缠
- 超导: 可集成化,相干性差,不好保持,最容易普及,可以做到”批量印刷”,2013年中国实现10个qubit超导线性方程计算(二元一次方程组求解,结果当时有误差),DARPA投资
- 量子点: 可集成化,相干性差,不好保持,DARPA投资