各类排序算法对比

本文最后更新于：2018年10月17日凌晨

我记得网络上流传有一个演示在不同情况下9种排序算法表现的视频，还挺有趣的，今天从原理、时间复杂度、稳定性、适用场景方面分别分析这9种排序算法。

前言

在此之前大家可以看下这个浅谈算法的BBC先回顾下:

(bilibili地址，这里不引用bilibili因为bilibili比较模糊)

BBC讨论概况:

通过一个小游戏讲述了算法在生活中的作用
从1964年诞生的冒泡排序算法开始介绍排序的算法
归并排序(拆分区域，分别合并有序的区域(由于有序对区域头分别对比即可)，展示了只要数据一多归并排序对比冒泡排序的优势就展示出来了
大概介绍了世界上有大约20种的排序算法
最短路径问题: 通过实验，展示了蜜蜂在寻找最短路径上的天赋，不过蜜蜂并不是找到最短的路径，而是对于其而言接近最短路径，换言之是足够短的路径

I. 各类排序应用场景对比

世界上有大于20种的排序排序算法，比如网络上就有23种排序算法比较的视频。

再比如该圆盘排序对比给了很多有趣的排序，下面对其中提到效率对比:

Double Selection Sort
Gravity Sort
Counting Sort
Radix LSD Sort(Base 4)
Radix LSD In-Place Sort (Base 10)
Radix MSD Sort(Base 4)
Time Sort(mul 4) + Insertion Sort

不过今天我们主要谈到常见的9种排序。对于排序而言其效率无法进行纯粹的对比，因为其涉及的纬度众多，比如数据量，原本的混乱情况，读写速度、处理速度等都会对其影响。

不过我们今天就对于混乱情况借助下面这个很有意思的视频，对其效率进行排序下:

效率排名	完全逆序	乱序	部分相同	几乎有序
1	快速排序(Quick)	快速排序(Quick)	快速排序(Quick)	插入排序(Insertion)
2	希尔排序(Shell)	希尔排序(Shell)	希尔排序(Shell)	鸡尾酒排序(Cocktail)
3	归并排序(Merge)	归并排序(Merge)	归并排序(Merge)	快速排序(Quick)
4	堆排序(Heap)	堆排序(Heap)	堆排序(Heap)	希尔排序(Shell)
5	梳排序(Comb)	梳排序(Comb)	梳排序(Comb)	归并排序(Merge)
6	选择排序(Selection)	插入排序(Insertion)	插入排序(Insertion)	梳排序(Comb)
7	插入排序(Insertion)	选择排序(Selection)	选择排序(Selection)	堆排序(Heap)
8	冒泡排序(Bubble)	鸡尾酒排序(Cocktail)	鸡尾酒排序(Cocktail)	冒泡排序(Bubble)
9	鸡尾酒排序(Cocktail)	冒泡排序(Bubble)	冒泡排序(Bubble)	选择排序(Selection)

	无序时间复杂度	有序时间复杂度	逆序时间复杂度
选择排序	$O(n^2)$	$O(n^2)$	$O(n^2)$
插入排序	$O(n^2)$	$O(n)$	$O(n^2)$
冒泡排序	$O(n^2)$	$O(n^2)$	$O(n^2)$

II. 各类排序详细分析

1. 选择排序 - Selection sort

选择排序-维基

原理

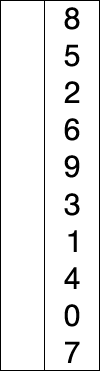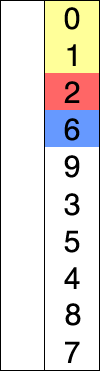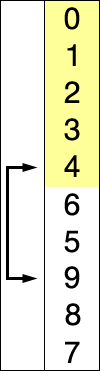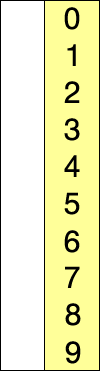
选择排序为众多排序里面最简单暴力的方案，简而言之就是每次找到最小的放到前面: 遍历长度为n的整个数组，第i次遍历，找到最小的（或最大）与i所在值进行替换。

每次交换情况:

5  6  1  8  2  4
↑     ↑
└─────┘
[1]  6  5  8  2  4
     ↑        ↑
     └────────┘
[1, 2]  5  8  6  4
        ↑        ↑
        └────────┘
[1, 2, 4]  8  6  5
           ↑     ↑
           └─────┘
[1, 2, 4, 5]  6  8
[1, 2, 4, 5, 6]  8
[1, 2, 4, 5, 6, 8]

效率分析

交换操作次数: [0, n-1] -> $O(n)$
比较次数: (n-1) + (n-2) + … + 1 = $n\frac{(n-1)}{2} -> $O(n^2)$
最好情况: 已经有序，交换0次
最坏情况: 交换$n-1$次
逆序交换: 交换$\frac{n}{2}$次
稳定性: 不稳定排序(由于每次交换前后顺序就被破坏)
时间复杂度: $O(n^2)$
空间复杂度: $O(1)$

横向对比

交换次数比冒泡排序少很多: 比冒泡排序快，由于交换所需CPU时间 > 比较所需CPU时间
当记录占用字节数较多时，通常比插入排序执行速度快些。

2. 插入排序 - Insert sort

插入排序-维基, 在几乎排列好的队列中效率最高，因为在有序的队列中，其完全不用赋值，只需要进行$n-1$次比较即完成排序。

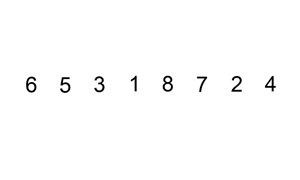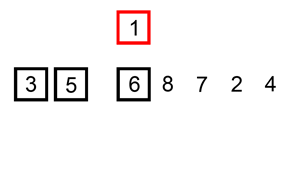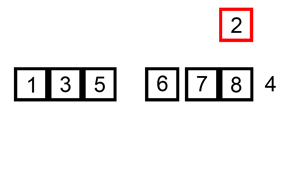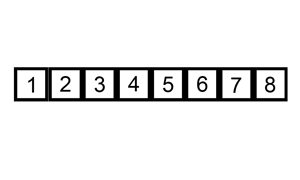
原理

插入排序的原理很想扑克牌抓牌，每次抓牌都是从桌面上的牌抓起插入已经排好序的手中的牌中: 往已经有序的数据序列中插入一个数，使得插入完成后依然有序。

每次交换情况(最坏也只需要$O(n)$次交换):

[5]  6  1  8  2  4
  ↑  │
  └──┘
[5, 6]  1  8  2  4
↑       │
└───────┘
[1, 5, 6]  8  2  4
        ↑  │
        └──┘
[1, 5, 6, 8]  2  4
   ↑          │
   └──────────┘
[1, 2, 5, 6, 8]  4
         ↑       │
         └───────┘
[1, 2, 4, 5, 6, 8]

效率分析

稳定性: 稳定排序
比较操作最好情况: 源数据有序，只需要$n-1$次
比较操作最坏情况: 源数据逆序，需要$\frac{1}{2}n(n-1)$次
赋值次数: $(比较操作次数) - (n-1)$ 因为$n-1$次循环中，每一次循环的比较都比赋值多一个，多在最后那次比较并不带来赋值
时间复杂度: $O(n^2)$ (最坏: $O(n^2)$; 最优: $O(n)$)
空间复杂度: 辅助空间$O(1)$

已有应用场景

由于其时间复杂度的缘故，不适合用于数据量较大的数据(如量级大于千)
在STL的sort算法和stdlib的qsort算法中被作为快速排序的补充，用于少量元素的排序(8个或以下)

public static void insertSort(int[] arr) {
  int length = arr.length();
  for (int i = 0; i < length - 1; i++) {
    int j = i;
    int tmp = arr[j + 1];
    for(; tmp < arr[j] && j >= 0; j--) {
      arr[j + 1] = arr[j]
    }

    // j = -1 or tmp >= arr[j]
    if (i != j) {
      arr[j + 1] = tmp;
    }
}

3. 冒泡排序 – Bubble sort

冒泡排序-维基

原理

从后往前分别两两对比，遇到前一个比后一个小，就进行交换，这样每一轮下来就会有一个最小数被交换到前面，以此类推。
冒泡排序只要数据一多，排序效率将会大打折扣，

每次交换情况(需要$O(n^2)$次交换):

5  6  1  8  2  4
         ↑  ↑
         └──┘
5  6  1  2  8  4
   ↑  ↑
   └──┘
5  1  6  2  8  4
↑  ↑
└──┘
[1]  5  6  2  8  4
              ↑  ↑
              └──┘
[1]  5  6  2  8  4
              ↑  ↑
              └──┘
[1]  5  6  2  4  8
        ↑  ↑
        └──┘
[1]  5  2  6  4  8
     ↑  ↑
     └──┘
[1, 2]  5  6  4  8
           ↑  ↑
           └──┘
[1, 2]  5  4  6  8
        ↑  ↑
        └──┘
[1, 2, 4]  5  6  8
[1, 2, 4, 5]  6  8
[1, 2, 4, 5, 6]  8
[1, 2, 4, 5, 6, 8]

效率分析

稳定性: 稳定排序(排序过程中，两两交换，相同元素前后顺序没有改变)
比较操作最好情况: 源数据有序，只需要$n-1$次(移动0次)
比较操作最坏情况: 源数据逆序，需要$\frac{1}{2}n(n-1)$次(移动$\frac{3}{2}n(n-1)$次)
时间复杂度: $O(n^2)$ (任何情况(源为逆序或正序): $O(n^2)$)
空间复杂度: 辅助空间$O(1)$

public static void bubbleSort(int[] arr){
  boolean changed;
  int len= arr.length;
  do{
    changed = false;
    len-=1;
    for (i = 0; i < len; i++) {
      // move larger one to next each time.
      if (arr[i] > arr[i+1]) {
        int temp = arr[i];
        arr[i] = arr[i+1];
        arr[i+1] = temp;
        changed=true;
      }
    }
  } while(changed);
}